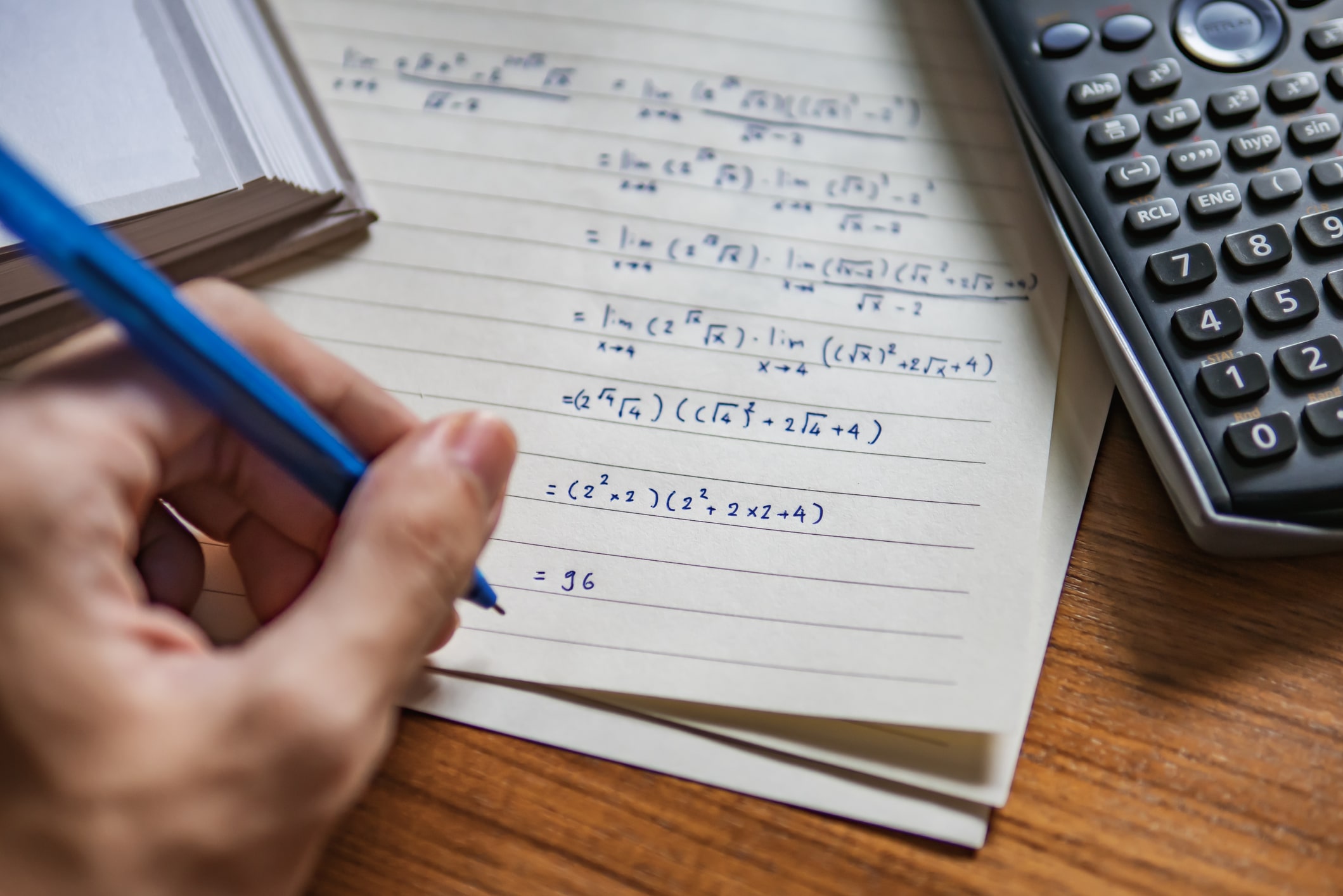
難関医学部合格を目指す受験生向けに、医学部受験の鍵とも言える数3の勉強法をご紹介します。

いつのタイミングで、どの順番で、どのように学習を進めていけば良いのでしょうか。

また、数3なしで受験できる医学部も解説しています。参考にしてみてください。

数3勉強のポイント3つ

数学、特に数3が得意になれるかは合格に大きく関わってきます。

一問あたりの配点が大きく、合否に大きく影響する数学ですが、その中でも医学部の数学では大きなウェイトを占めるのが数3の分野です。

数3は、発想力よりも論理と正確さが求められます。

論理的な思考力と膨大かつ正確な計算を要求される物理、化学においてもこの力は活きます。

では医学部受験の鍵となる数3の勉強法を紹介していきます。

学習するうえで心がけて欲しいポイントが3点あります。

①煩雑な計算を正確に解く計算力

微分・積分、極限の計算、極形式は複雑な式変形、指数の見落とし、符号の間違いなど、ケアレスミスが多い分野です。

②解法パターンの暗記

数3は問題文をパターン化して解法に落とし込めれば、あとは①の計算力でごり押すことができます。

③各分野のつながり

基礎となる数1A、数2Bとのつながり、そして数3の中でも各分野のつながりを意識しましょう。

数3を学習する中で、関連する他の分野も復習していくことで、数学の力全般の底上げにもつながります。

数1A、数2Bを完璧にしてから、と思わず、並行して取り組むと良いです。

分野別の勉強法

次に各分野の基礎を押さえていきましょう。

各分野を取り組むうえで、つまづく箇所があったら必ず数1A、数2Bに戻って復習しましょう。

関連する数1A、数2Bの分野を併記しました。

関数

より複雑な形の関数を扱います。

単体での出題は少なく、極限、微分・積分の分野で重要になってきます。

・分数関数
・無理関数
・逆関数
・合成関数
　→2次関数

数列と関数の極限

今までは有限個の数列を扱いました。

数列を無限に続けていくとどうなるでしょうか。

極限はグラフをイメージすると考えやすいです。

・色々な関数の極限
・無限級数の収束と発散
・漸化式と極限
・中間値の定理
・はさみうちの原理と追い出しの原理
・区分求積法
　→場合の数、確率、数列と漸化式

微分・積分とその応用

整式以外の微分・積分法もおさえましょう。

計算問題、証明問題、図形問題に分けられます。

・図形の面積、体積、弧の長さ
・微分方程式、積分方程式
・微分不等式、積分不等式
・陽関数表示と陰関数表示
・平均値の定理
・近似式
　→整式の微分・積分

複素数平面

複素数平面を導入することで、より複雑な図形の操作も簡単に行うことができます。

・複素数平面上での図形の表し方
・極形式の計算（積、商、ド・モアブルの定理）
・極形式を用いた回転、拡大、縮小
・変換、反転
　→複素数と方程式、平面ベクトルと平面図形、三角関数

平面上の曲線

数2範囲の図形と方程式より複雑な図形が登場します。

一見全く違ったものに見える図形が、実は同種の円錐曲線であるという面白さがあります。

複素数平面における極形式の考え方と関連します。

・2次曲線（放物線、楕円、双曲線）の方程式
・焦点、接線、漸近線の求め方
・曲線の媒介変数表示、極方程式
・離心率による定義
・複素数平面上での回転、拡大、縮小
・最大、最小
・軌跡と領域
　→2次関数、図形と方程式

まずは比較的馴染みのある関数、数列と関数の極限から取り組むと良いでしょう。

そして入試で最も出題頻度の高い微分・積分とその応用に取り組みましょう。

早いうちから始めて得点源にできると強みになります。

そして最後に複素数平面と平面上の曲線です。

この2つの分野は密接に関連していて、複合的な問題が出題されることも多いです。

教科書で扱われる範囲はあまり広くない一方で、代数的側面と幾何的側面を持ち合わせた複素数平面は、大学入試においては出題範囲も多岐に渡ります。

他分野の深い理解も欠かせないので最後に学習すると良いでしょう。

発展として、重積分、パップスギュルダンの定理、チェビシェフ多項式、ヤングの不等式、ベータ関数、ガンマ関数など、大学範囲の数学をもとにした問題が出題されることもあります。

このような問題には、知らなくても誘導に乗れば解ける問題と、背景を知っていると有利になる問題の2種類があり、知らないと解けない問題はほぼ出題されないので安心してください。

演習を重ねるうちに、同じ数学的知識をもとにした問題が繰り返し出題されていることに気づくでしょう。

出てきた時にその都度、頭の片隅にストックしていくと良いです。

対策を始める時期

では、いつからどのように対策を始めれば良いのでしょうか。

通常、数3は高校3年生の授業で扱われる科目ですが、これでは間に合いません。

難関医学部を目指すのであれば、高校2年生の夏頃からは数3を始めたいものです。

数3の土台となるのは数1A、数2Bだというお話をしました。

すると、高2の夏までには数1A、数2Bの標準的なレベルの入試問題を解けるレベルになっておきたいですね。

という様に、受験までの年数から逆算していつまでに何を勉強するべきか計画を立てましょう。

まずは大きな最終目標（ここでは難関医学部合格）を立て、そこから遡って小さな目標とその目標を達成するためのプランを考えると良いでしょう。

そうして理想の計画通り学習を進められれば、高校2年生が終わる頃には数1A、数2Bの標準的〜難問レベルの入試問題を解く力と、数3の基礎が身についていることでしょう。

高校2年生のうちに数学の力をある程度完成させておくことで、高校3年生の1年間を丸々演習、志望校対策に費やすことができます。

数3なしで受験できる医学部の大学（国立・公立）

医学部を設置している国公立大学を、数3なしで受験できるパターンについては、学科や専攻により大きく4つに分けることができます。

・医学科

→数Ⅲなしでの受験は後期日程に多い

公立大学の中には数Ⅲなしで受けられる医学科はないので、国公立を受けるのであれば国立を目指すことになるでしょう。

・看護学科・看護学専攻

→前期日程や後期日程に関係なく数Ⅲなしでの受験ができる

・理学療法学、作業療法学を専攻

→前期日程や後期日程に関係なく数Ⅲなしでの受験ができる

・検査技術科学、放射線技術科学を専攻

→医学科と同じく後期日程で数Ⅲなしが多い

・保健学科

→医学科以外の上記の専攻が含まれているので、大学によってばらつきがあります。

医学部を設置している国公立大学のほとんどで、数Ⅲなしの受験をすることはできますが、医学科に絞るとその学校数は激減します。

さらに医学科を受けるのであれば、前期日程に数3は必須。

前期日程の2次試験の中で数3が課せられるので、後期日程のみで数3なしの受験となる大学が多いです。

日程に関係なく数3なしの受験ができる医学科は少なく、大半が看護学を学ぶ学科やコースとなります。

もしくは理学療法学や作業療法学を専攻にする場合に、日程に関係なく数3なしの受験が可能なところが多いです。

検査技術科学、放射線技術科学を学ぶのであれば、医学科と同じように基本的には数3が課されることが多く、募集しているのは後期日程となります。

後期日程にして数3なしを狙おうと考える方もいると思いますが、前期日程とは募集人数に大きな違いがあるので注意が必要です。

前期日程の募集人数が、後期日程の募集人数の5倍以上になっている所も珍しくありません。

自分が受けようと思っている大学の募集要項はしっかりと確認しましょう。

都道府県	大学名
北海道	北海道大学旭川医科大学
青森県	弘前大学
宮城県	東北大学
秋田県	秋田大学
山形県	山形大学
茨城県	筑波大学
群馬県	群馬大学
東京都	東京医科歯科大学
新潟県	新潟大学
富山県	富山大学
石川県	金沢大学
福井県	福井大学
山梨県	山梨大学
長野県	信州大学
岐阜県	岐阜大学
静岡県	浜松医科大学
愛知県	名古屋大学
三重県	三重大学
滋賀県	滋賀医科大学
大阪府	大阪大学
兵庫県	神戸大学
鳥取県	鳥取大学
島根県	島根大学
岡山県	岡山大学
広島県	広島大学
山口県	山口大学
徳島県	徳島大学
香川県	香川大学
愛媛県	愛媛大学
高知県	高知大学
福岡県	九州大学
佐賀県	佐賀大学
長崎県	長崎大学
熊本県	熊本大学
大分県	大分大学
宮崎県	宮崎大学
鹿児島県	鹿児島大学
沖縄県	琉球大学

数3なしで受験できる医学部の大学（私立）

医学部を設置している私立大学は31校ありますが、数3の試験を課していない大学は2校です。

いずれの大学でも数3なしで医学部医学科を受験することができます。

ちなみに国公立大学では医学科以外にも看護学科や保健学科の数3なしでの受験ができるのですが、私立大学では医学科のみです。

両大学では偏差値や、6年間の学費に関して大きな差はありません。

立地については帝京大学は東京都に、近畿大学は大阪府にあるので、大学進学を機に地方から都会へ引っ越したいと考えている学生も受けやすいでしょう。

帝京大学医学部のキャンパスは郊外にあるわけではないので、授業終わりや休日に出かけやすい立地です。

周囲にはお店もたくさんあります。

近畿大学医学部では、緑に囲まれたキャンパスに通うことになります。

大学周辺は帝京大学のキャンパスほど充実していないものの、電車を利用すれば繁華街まで行けるので、都会と郊外の両方を楽しむことができます。

国公立の医学科を受験する場合、前期日程では数3が必要です。

どうしても数3を使わずに医学部、特に医学科に行きたい人には、私立の帝京大学や近畿大学がおすすめです。

両学とも偏差値は66前後であり、医学部受験としての難易度が極めて難しいという訳ではないので、国公立大学にこだわりがなければ検討してみても良いでしょう。

＜私立＞

都道府県	大学名
東京都	帝京大学
大阪府	近畿大学

数3なしで医学部受験をすることは可能です。

私立大学では2校でしたが、国公立ではほとんどの大学で数3なしの受験ができます。

学科や専攻するコースによって、「後期日程のみで数3なし」なのか、「前期日程でも数3なし」なのか変わってきます。

また前期日程と後期日程では募集人数が異なることも多いので、自分が受けたい大学、学科の募集要項は必ずしっかり確認しておきましょう。

関連コラム：医学部の受験科目は？国公立・私立それぞれ解説